椭圆曲线

四省联考给我们带来的备考启示

如果大家喜欢本文，欢迎点赞或者赞赏！谢谢支持！

目录:

• 1. 部分试题讲解
• 2. 对备考的启发
  
  

1 部分试题讲解

8. 已知满足, , 则

• A. ,
• B. ,
• C. ,
• D. ,

答案： B.

提示： 由题意, , . 这里有两个方程、三个未知数, 可通过让一个数取某个特殊值来确定其余值. 注意是上述方程的一个解, 无法排除任何选项. 我们可以考虑让某个数非常大, 比如让, 那么也很大, 从而只需“抓大头”:

于是, 注意, 所以

于是, , , 解得, . 所以, . 所以选B.

注： 事实上, 当时, 可用计算器计算得, , 和我们的估计值差不太多.

答案： ABD.

解： 我们定义从实数到点的函数表示点. 于是是周期为的函数.

由题意, 起始点是, 起始点是. 假设与重合时经过了秒, 则旋转了个弧度, 旋转了个弧度. 而与重合当且仅当的弧度相差的整数倍, 即

所以. 此时, 点位于

把A,B,C,D选项写成的形式分别为:

定义点列, . 由于周期是, 故

则周期为3. 而等于A选项, 等于B选项, 等于D选项, 故答案为ABD.

注：寻找模型的周期性在2009年福建高考第15题就考过，可阅读：

往年高考原题精选(12)——周期数列

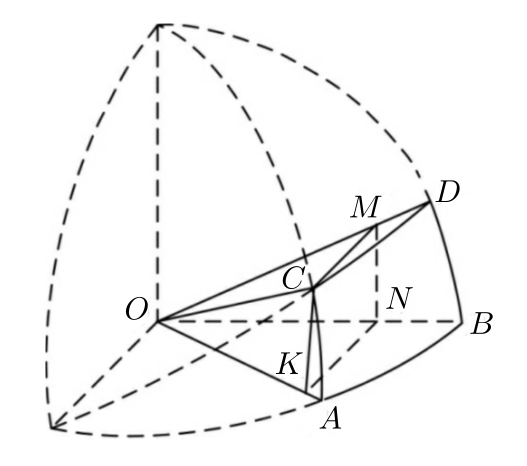
12. 下图改编自李约瑟所著的《中国科学技术史》，用于说明元代数学家郭守敬在编制《授时历》时所做的天文计算. 图中的, , , 都是以为圆心的圆弧,是为计算所做的矩形, 其中分别在线段上,, . 记, , ,, 则

• A.
• B.
• C.
• D.

答案： ACD.

解： 由题意, 且, 且

逐一验证四个选项即可:

• A选项:.
• B选项:.
• C选项:.
• D选项:.

因此选ACD.

15. 数学家祖冲之曾给出圆周率的两个近似值: “约率”与“密率”. 它们可用“调日法”得到: 称小于3.1415926的近似值为弱率, 大于3.1415927的近似值为强率. 由, 取3为弱率, 4为强率, 得, 故为强率, 与上一次的弱率3计算得, 故为强率, 继续计算, ……. 若某次得到的近似值为强率, 与上一次的弱率继续计算得到新的近似值; 若某次得到的近似值为弱率, 与上一次的强率继续计算得到新的近似值, 依此类推. 已知, 则  _____________ , _______________.

答案： ; .

解: 依题意, 记第次运算后得到的弱率为, 强率为, 其中是正整数. 则定义. 若, 则记新的强率为, 而弱率不变, 即; 若, 则记新的弱率为, 而强率不变, 即. 如此可以定义运算法则. 经过计算, 可得下表:

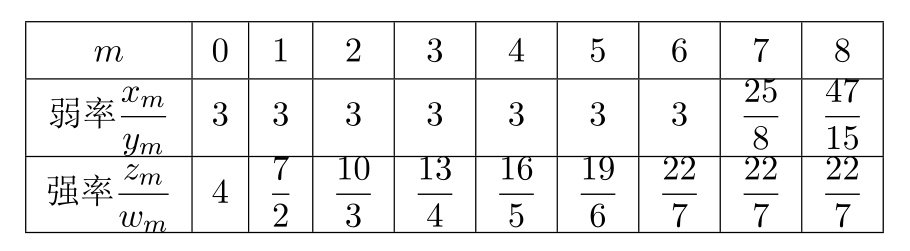
其中, 在第7步算出后, 是弱率, 而是强率, 因此. (无需再比较与3.1415926的大小)

注： 思考题：请算出中第几项是?

16. 右图为一个开关阵列, 每个开关只有“开”和“关”两种状态, 按其中一个开关1次, 将导致自身和所有相邻的开关改变状态. 例如, 按将导致, , , , 改变状态. 如果要求只改变的状态, 则需按开关的最少次数为___________.

(1,1)	(1,2)	(1,3)
(2,1)	(2,2)	(2,3)
(3,1)	(3,2)	(3,3)

答案： 5.

解: 把9个开关分成两组: A组是, , , ; B组是, , , , . 按下A组开关可改变偶数个开关的状态, 按下B组开关可改变奇数个开关的状态. 若只改变的状态, 则B组开关必须按下奇数次. 另外, 按下同一个开关两次不会改变任何状态, 所以为了让次数尽可能小, 每个开关最多只按一次.

基于上面的观察, 注意到按下, , , , 可使得最终只改变的状态, 并且不存在按开关次数更少的方法. (可用穷举法说明)

20. 一个池塘里的鱼的数目记为, 从池塘里捞出200尾鱼, 并给鱼作上标识, 然后把鱼放回池塘里, 过一小段时间后再从池塘里捞出500尾鱼, 表示捞出的500尾鱼中有标识的鱼的数目．
(1) 若, 求的数学期望;
(2) 已知捞出的500尾鱼中15尾有标识, 试给出的估计值. (以使得最大的值作为的估计值)

解： (1)的所有可能取值是, 并且分布列为

因此服从超几何分布, 且, , , 从而

(2)当时, 捞出的500尾鱼至少有16尾有标识, 因此.

当时, . 记. 根据

可知

由当且仅当, 可知当时, ; 当时, , 故时最大, 所以的估计值为.

注： 此题背景是“极大似然估计”，我曾经写过文章介绍：

高考题中的高等背景(6)——极大似然估计（2018年全国Ⅰ卷第20题）

22. 椭圆曲线加密算法运用于区块链.

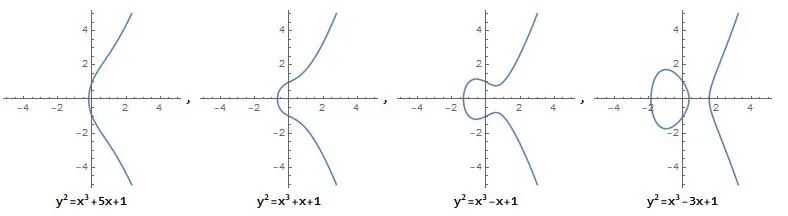
椭圆曲线. 关于轴的对称点记为.在点处的切线是指曲线在点处的切线. 定义“”运算满足：①若, , 且直线与有第三个交点, 则; ②若, , 且为的切线, 切点为, 则; ③若, 规定, 且.

(1) 当时, 讨论函数零点的个数;

(2) 已知“”运算满足交换律、结合律, 若, , 且为的切线, 切点为, 证明：;

(3) 已知, , 且直线与有第三个交点, 求的坐标.

参考公式: .

【参考答案】

(1)由题设, , . 令, 可得, .

当时, 时, 单调递增; 时,单调递减; 时, 单调递增.

当, , 所以有2个零点. 当, , 所以有2个零点.

当, 有, 则有1个零点.

(2)因为为在点处的切线, 且, 所以, 所以

两边作用可得

即, 故.

(3)直线的斜率. 设与的第三个交点为, 则

代入可得

代入可得

同理可得

两式相减可得. 因此的坐标为

注： 第(3)问也可以用三次方程的韦达定理. 具体思路：首先, 由在上可得

其中, 三点共线, 位于直线上, 其中根据①②相减,  利用立方差公式可得

所以于是, 联立方程

消去可得

化简得

由于是这个方程的三个根, 因此由三次方程韦达定理可得

接下来步骤与参考答案一样.

2 对备考的启发

我在这篇文章解读了2023年高考数学的趋势，我在里面曾经说了下面几点：

1. 今年高考命题会更加注重高中到大学的衔接，在大学用不到的内容可能会少考一点、在大学用得多的内容可能会多考一点。甚至可能会有更多的大学知识下放。注意，大学知识不一定是指大学的数学知识，像天文学、大气科学、医学、计算机科学等知识也可能会下放，然后用所学的高中数学知识解答！！（椭圆曲线是密码学的内容，而密码学跟计算机科学密切相关！）

2. 逻辑推理是是人们在数学活动中进行交流的基本思维品质。2023年与之前相比会注重考察思维，应该不会再像2022年新全国1卷那样计算量极其恶心，取而代之的是计算量的减少、思维量（即逻辑推理的含量）的提升。当然，同学们一定不能疏忽计算能力的训练，而要同时抓计算能力和数学思维。

这次的题目，如大家所见，计算量并没有2022新高考全国Ⅰ卷那么大。取而代之的是，这份卷阅读量很大，新的信息很多，更倾向于考察同学们逻辑推理能力与学习能力(信息转化能力)。

备考建议

如果你挣扎于及格线以下，接下来赶紧去补基础，争取把基础题拿下。

如果你想突破120分，那接下来应该往哪个方向备考？

一、提升逻辑推理能力

同学们要下意识地练习证明题，课本上就有不少证明题了，一定要反复琢磨。

这份卷从第7题开始就处处充满了对逻辑推理的考察要求。

二、回归课本，回归基础

教材是最好的备考素材，请同学们要至少看一遍所有课后习题，自己把“看上去没思路”的题多做几遍，争取能自己做得出来。除此之外，教材上的“阅读与思考”、“探究与发现”等内容非常重要，同学们一定要仔细阅读并思考这部分内容，多想想“为什么”。

比如，第20题（概率题）有很多同学可能无从下手，其实这题考察了证明数列单调性的方法以及超几何分布，书上有几乎一模一样的叙述。超几何分布单纯是考察定义与性质，而证明数列单调性的方法位于人教A版“二项分布与超几何分布”一节的“探究与发现”部分(82页)：

超几何分布的定义(人教A版选择性必修三第78页)

单调性(人教A版选择性必修三第82页)

三、提升阅读量和学习能力

这次的11、12、15、16、22题都是阅读量极大的题目。同学们如果想突破120分，不能惧怕阅读题干较长的题目，而是要迎难而上，抽丝剥茧般分析题目究竟想表达什么意思。这对同学们的学习能力提出了较大的要求。而学习能力恰好符合《教育部关于做好2023年普通高校招生工作的通知》中提到的“服务人才培养质量提升和现代化建设人才选拔”的选拔要求。

比如这里第22题(2)问的证明题非常陌生，没法用所学知识解答。那很自然的，只能用题目所给的信息解答了。

结合已有的学习资料去梳理一些经典题型的备考方式只是在提升同学们的归纳总结能力，并不能有效提升自己的学习能力。如果在备考过程中一直把时间花在梳理经典题型上，只能让自己对高中数学内容产生刻板印象（即哪些知识必考、哪些知识必不考等错误观念）。只有面对新知识的时候知道怎么去处理它们、应用它们，才能提升学习能力。所以同学们要适当地阅读与数学有关的文本。

同学们在备考过程中，可以尝试去阅读我整理的“高考题中的高等背景”栏目，相信这对同学们的视野提升会有所帮助。

分形（人教B版必修第四册39-40页）

四、提升数感

第8题如果想着所谓的“同构”去解答，几乎是没办法解出来的。

这里说个题外话：我个人并不喜欢把构造同样结构的表达式的解题技巧称为“同构”, 这跟抽象代数里面的“同构”并不是一个意思。

类似地，“椭圆曲线”并不是形如椭圆的曲线，我想这份卷出“椭圆曲线”可能就是为了纠正目前许多老师和同学都犯的名词混用的错误。（很多同学甚至老师都把形如椭圆的曲线称为“椭圆曲线”）

如果想解出第8题，需要会对数字作简单的估计。同学们要通过“找大头、去尾”的方式来估计数据，这样能节约解题时间。这个往年高考也考过许多次，比如，在往年高考中，2019年课标全国Ⅰ卷第4题、2019年课标全国Ⅱ卷第4题、2022年北京卷第7题、2022年新高考全国Ⅰ卷第4题都考察了这一点。

【注】转自《Fiddie高中数学杂谈》。