嗨,朋友们,好久不见,已经很久没有更新公众号了,但其实在写贝叶斯的时候,我已经想好了这一篇写「关联规则」,因为其中也会涉及到条件概率,而且两者都属于数据挖掘领域。那话不多说,我们就开始这一次的统计之旅吧~
关联规则分析又称为购物篮分析,最早是为了发现用户超市购物篮里商品的关联关系,进而用来分析用户的购物行为。美国沃尔玛超市曾意外发现,跟尿布一起购买最多的商品竟然是啤酒,产生这一现象的原因是:美国人常叮嘱丈夫下班后为小孩买尿布,而丈夫们往往会随手带回他们喜欢的啤酒,这就是统计人听到吐的「啤酒与尿布」的故事。
之前也浅讲过推荐的协同过滤算法,如何找到商品的相似商品,那这里从理论上来说啤酒和尿布也可以被计算为相似商品(同时被多个用户所行为),那关联规则属于推荐领域吗?我认为不是,因为关联规则的重点在于规则,而非关联,例如规则A、B=>C,其中A、B称为前项,C称为后项,该规则表示购买A、B的用户还会购买C。
既然作为规则,那一定有相应的评价方式,来判断「规则是否可以成为规则」,也就是规则的两个评价指标,支持度和置信度。支持度用来衡量商品集合出现的频繁程度,置信度则用来衡量规则的可信程度,两者表示规则需要是频繁的、可信的。
以一个事务项为例,每一行记录可以看作是一个购物篮
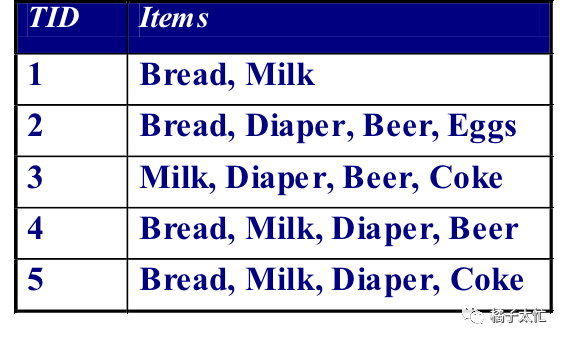
规则Bread、Milk=>Diaper的支持度为2/5(Fraction of transactions that contain Bread&Milk&Diaper),置信度为2/3(how often Diaper appears in transactions that contain Bread&Milk),这里置信度的计算公式就是条件概率的计算公式,P(A|B) = P(AB) / P(B),其中A = Diaper,B = Bread&Milk,在实际应用中,需要人为事先给定支持度和置信度的阈值,规则同时满足最小阈值条件即可。
在搞清楚规则的生效标准之后,我们再来详细讲讲如何从万千数据中找出有效的关联规则,这里要讲到的算法是Apriori,是关联规则中最为基础、简单、经典的一种算法(主要其他我也不太熟,该算法的核心思想是逐层搜索后迭代,关键方法是剪枝。
我们从两个评价指标中也不难想到算法实现的具体步骤,第一步先找到由商品组成的所有频繁的项目集合,第二步再从频繁集中找到所有可信的规则,例如{a,b,c}是一个频繁集,那么存在的潜在规则有{a}=>{b,c}、{b}=>{a,c}、{a,b}=>{c}、{a,c}=>{b}等等。
首先,找到所有频繁的项目集合,最简单粗暴的方式,就是列举出所有商品的可能组合,再依次计算每个组合的支持度,过滤掉低于阈值的组合。但我们通过数理知识可以知道,当商品数为n时,可列举的商品组合数为2^n-1,例如商品{ABCDE}的可列举组合如下:
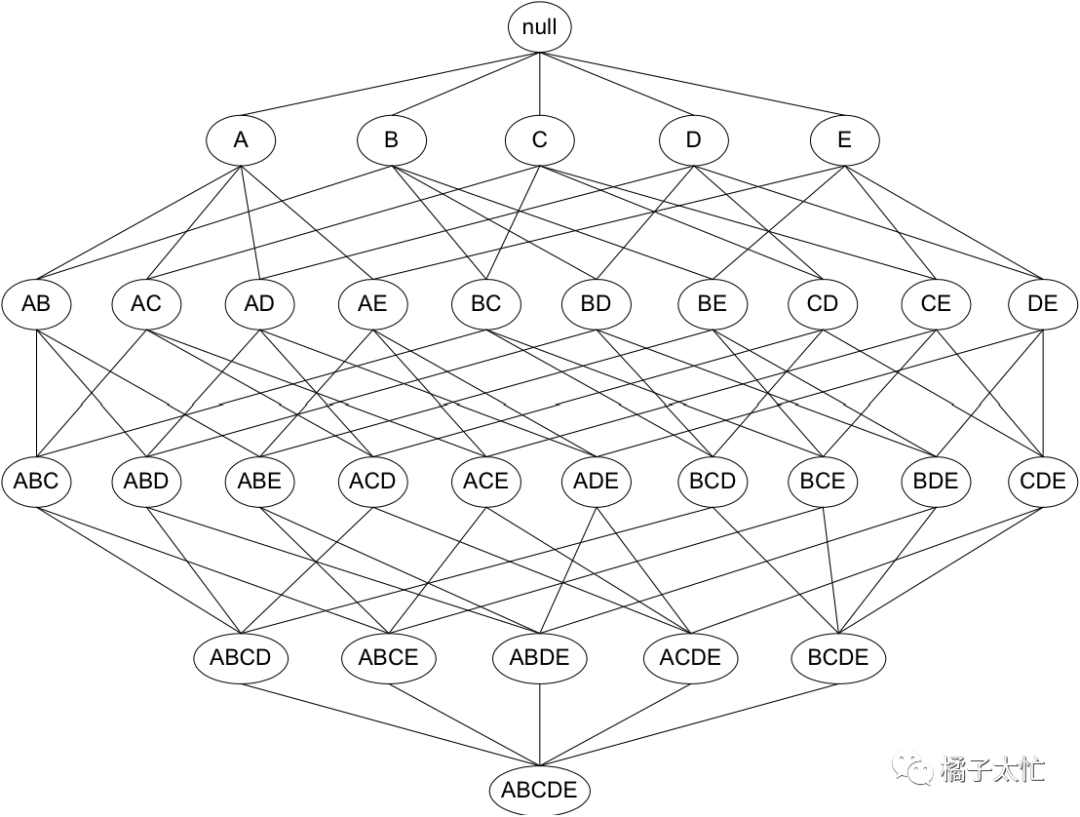
当商品数增加时,可列举的商品组合数是呈指数级增长的,这对于算力来说无疑是灾难级的,而Apriori的剪枝算法就是用来解决这个问题的。从人类常识可知,如果一个集合是频繁的,那么它的子集也一定是频繁的。对应的数学表达式为:
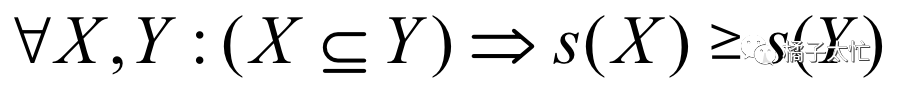
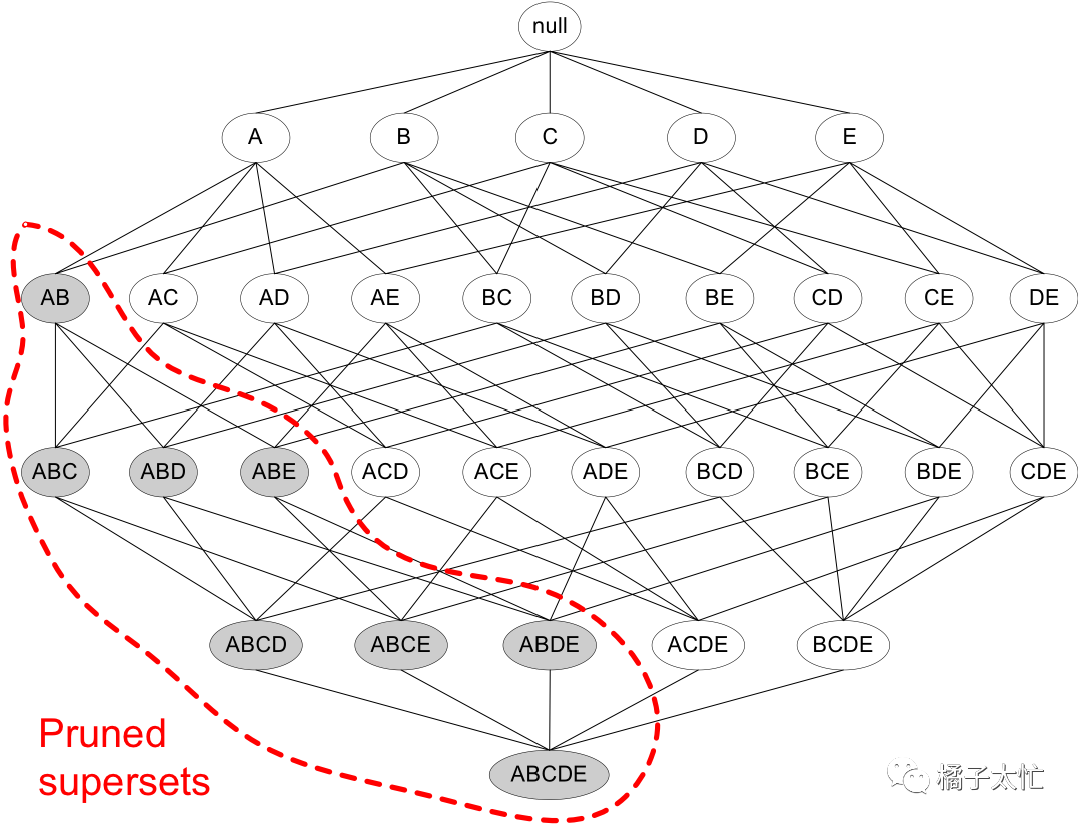
S为支持度,我们也把这个性质称之为反单调性性质,做过逻辑题的同学应该知道,原命题和逆否命题的关系为等价的,那么我们就可以推出剪枝口诀为:如果一个项目集是不频繁的,那么它的超集也一定是不频繁的。如下图所示,如果AB的支持度是不频繁的,那么它对应的所有超集都可以被剪掉。
关键方法讲了,我们再来结合例子讲一讲逐层搜索后迭代的思想。沿用上面的例子,我们先假定支持度的阈值为3,从商品组合数为1开始迭代:
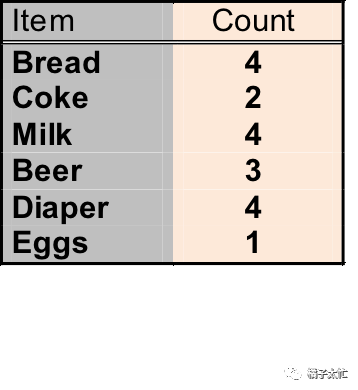
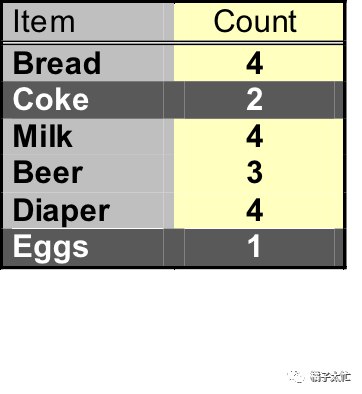

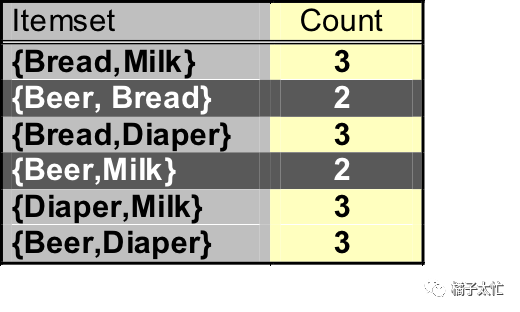
可以看出第一次迭代剪掉了coke和eggs,剩下4个商品经过组合后,第二次迭代又剪掉了{beer、bread}和{beer、milk},如果我们不用剪枝算法的话,假设迭代三次,蛮力生成的组合数为C6^1+C6^2+C6^3=41种,剪枝后就变为C6^1+C4^2+C4^3=16种,是不是很简单(摊手。
另外,在层层迭代生成候选集组合时也有一定的剪枝技巧,如果暴力循环遍历会导致组合的重复生成,具体的实现方式是,如果两个Fk-1(商品组合数为k-1的频繁集)的前k-2项商品是一致的,那么就可以把两者拼在一起构成Fk。例如有一个3项的频繁项目集F3为 {ABC,ABD,ABE,ACD,BCD,BDE,CDE},那我们只需要拼接:(ABC, ABD)、(ABC, ABE)、(ABD, ABE),对应生成F4为{ABCD、ABCE、ABDE},由于BCE和ADE不在F3中,即这两个商品组合是不频繁的,那么它们对应的超集ABCE和ABDE也是不频繁的,剪枝后仅剩下ABCD。
完成第一步动作后,从一定程度上来说,频繁集可以看作是相似商品的组合,不过我们的重点是要基于频繁集来生成规则。当某个频繁集的商品数为n时,对应可生成2^n-2对规则(为什是-2,规则需要有前项和后项,要减去空集和全集),of course!第二步也有对应的剪枝技巧。
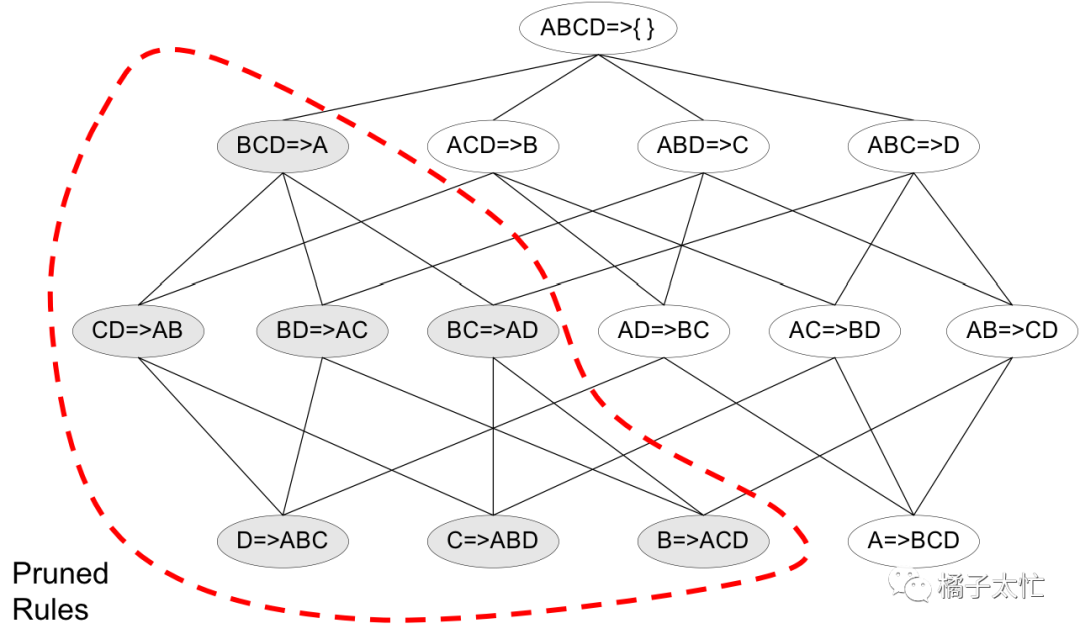
例如频繁集{ABCD}就有c(ABC —> D) ≥ c(AB —> CD) ≥ c(A —> BCD),其中c为置信度confidence。原理很简单,我们转化成条件概率的公式就可以明白,分子均为P(ABCD),分母依次为P(ABC)、P(AB)、P(A),某个集合的频数一定是比它的子集更小的,那么就有P(ABC)<P(AB)<P(A),从而可以推出规则的剪枝公式。如果c(ABC —> D)的置信度是不符合阈值要求的,那么我们就可以把等式右边相应规则都剪掉,如下图所示:
到此,什么是关联规则,关联规则是不是推荐,规则的评价指标是什么,以及过程如何实现的(迭代+剪枝),我想都已经讲得很清楚了。
这篇文章的第一行是在端午节假期写下的,在那个当下我就想好了下一篇写什么,就像我和李女士相约宁波时,也规划好了下一次的相聚地,怎么说呢,不确定的人生轨迹里,零星两点确定的期许也会让人感到幸福吧。
写完这一篇,2023也过去一半了,人有的时候会在某个固定的节点来看自己的变化,但其实对于这一刻我变成什么样子,好像并没有那么重要,过去这半年不断迷失又找到自我、认识自我的过程才是最伟大的。
最后,希望下半年的生活一切顺利,能在工作之余抽出时间多看书多写写东西,毕竟唯有热爱可抵岁月漫长。

